5 Describing a nitrogen budget
Background Readings:
- pp. 17-35 (Soetaert and Hermann 2009)
- Bormann et al. 1977. Nitrogen Budget for an aggrading northern hardwood forest ecosystem. Science 196:981-983.
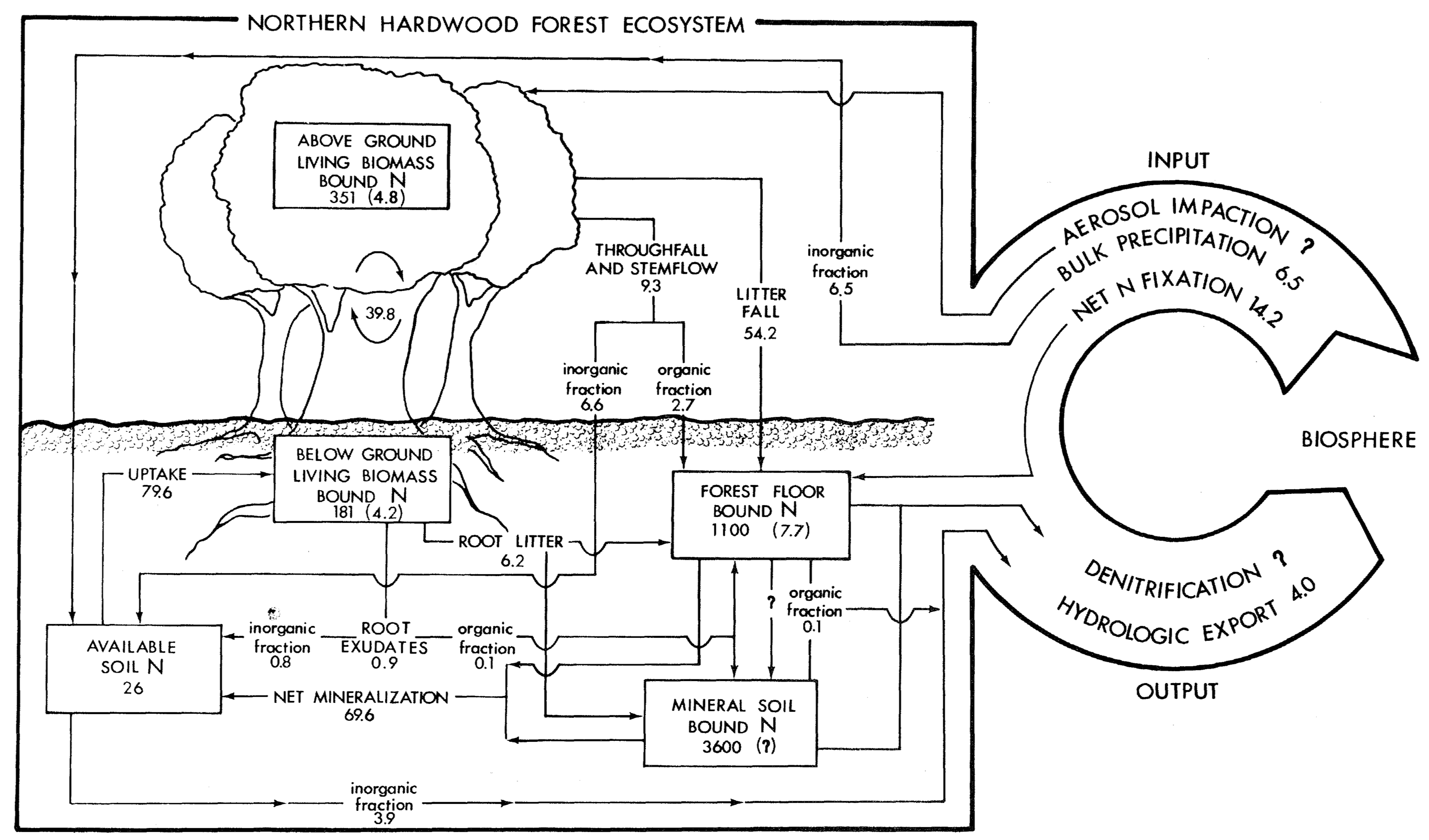
Figure 5.1: Nitrogen budget for a temperate northern hardwood forest (Hubbard Brook Watershed 6, Bormann et al. 1977).
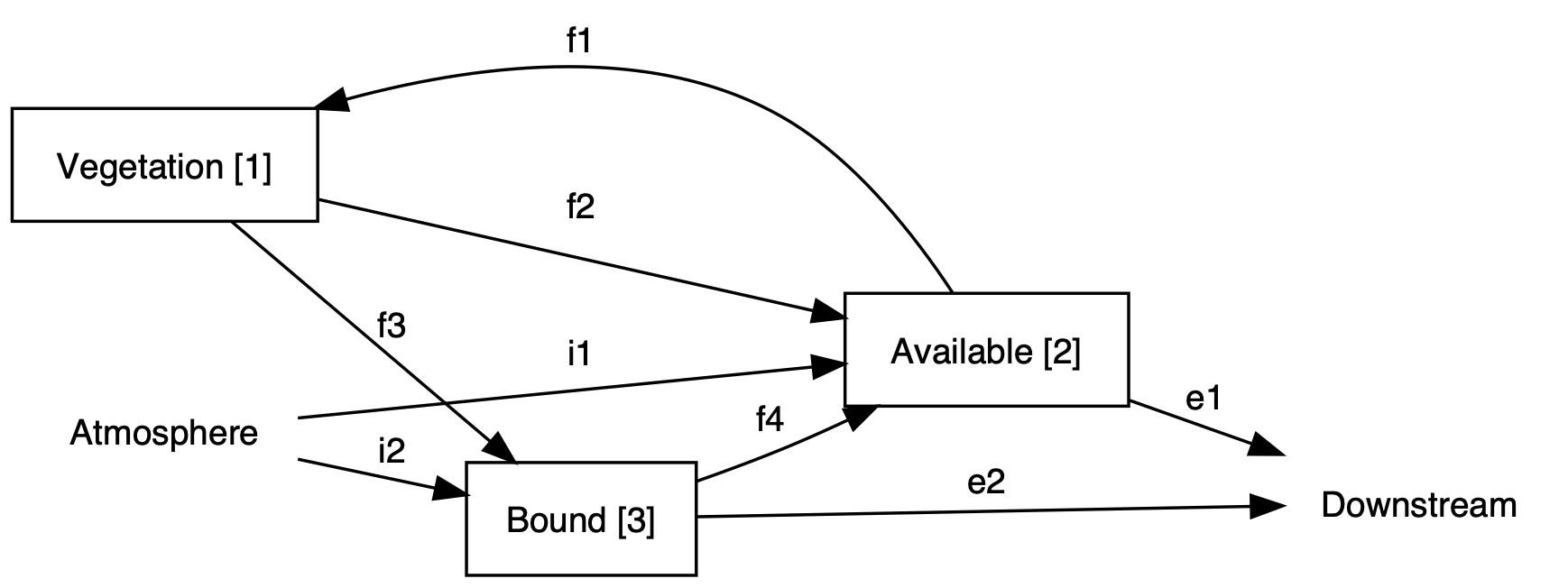
Figure 5.2: A simpler compartment model for Hubbard Brook Watershed 6, based on Bormann et al. (1977).
5.1 Getting started
(S&H 15-17) For any ecosystem, we want to start with paper and pencil and sketch out the pools and the fluxes that we think are important (see example, Fig. 5.2). Don’t sweat the details yet – you’ll revise it anyway. Go ahead an label the compartments and the fluxes with with both biological and physical processes as well as some simple abstract notation.
Write balance equations (S&H, 3, 17-20). For each flux, identify the underlying biological and physical processes. If you don’t completely know, don’t sweat it. Here are the balance equations for Fig. 5.2:
Rate of change of vegetation = uptake - exudates and through fall - leaf and root litter loss \[\frac{dV}{dt} = f_1 - f_2 - f_3\]
Rate of change in available pool in soil solution = bulk precip + exudates and through fall + net mineralization - uptake - stream export \[\frac{dA}{dt} = I_1 + f_2 + f_4 - f_1 - E_1\]
Rate of change in the bound pool = net N fixation + leaf and root litter loss - net mineralization - stream export \[\frac{dB}{dt} = I_2 + f_3 - f_4 - E_2\]
- Assess the total load or mass budget (S&H, 19-22). For Fig. 5.2, we have \[\frac{d\left(V+A+B\right)}{dt} = \frac{dV}{dt} + \frac{dA}{dt} + \frac{dB}{dt} = (f_1 - f_2 - f_3) + (I_1 + f_2 + f_4 - f_1 - E_1) + (I_2 + f_3 - f_4 - E_2)\] \[\frac{d\left(V+A+B\right)}{dt} = I_1 + I_2 + f_1 - f_1 + f_2 - f_2 + f_3 - f_3 + f_4 - f_4 - E_1 - E_2\]
\[\frac{d\left(V+A+B\right)}{dt} = I_1 + I_2 - E_1 - E_2\] From this we see that the total mass budget for this watershed depends simply on import or inputs, and exports or outputs.
- For each flux, decide which pools directly influence the flux. In a forest, the flux of nitrogen from vegetation to soil will depend enormously on the amount of vegetation present as leaves senesce and fall, fine roots die back, and water leaches nutrients out of leaves and bark. The flux is very unlikely to depend directly on the amount of nitrogen already in the soil. In a lake, the flux of phosphorous from the water column into phytoplankton depends on the amounts of both the amount of phytoplankton and the amount of phosphate in the water at any given instant.
For the vegetation pool in Fig. 5.2, we see each flux (\(f\)) is a Function (\(F()\)) of one or two pools:
- Uptake: \(f_1 = F(V,A)\)
- Leaf and root litter, and throughfall: \(f_3 = F(V)\)
- Root exudates, and throughfall: \(f_4 = F(V)\)
Next, we want to represent these fluxes in a mathematical form.
5.2 Mathematical forms
A common starting point for dynamics depending on two pools is the law of mass action. This states that the reaction rate is proportional the product of the pools. In the case of plant uptake of N, which depends on the amounts of N in the available pool and the vegetation pool, this would be \(aVA\), where \(a\) is a proportionality constant. In some circumstances, these pools might also have exponents different than one (\(aV^1A^1\)), such as \(aVA^2\). This occurs in chemistry when a reaction requires two molecules of “A” for each molecule of “V”. It might occur in ecology if a rate depends differentially on A and B.
Using the law of mass action for plant uptake, we will describe the fluxes in the simple N budget above (Fig. 5.2) with the following expressions.
\[\begin{align} \frac{dV}{dt} &= a_{1}AV - a_{2}V - a_3 V\\ \frac{dA}{dt} &= I_1 + a_{2}V + a_{4}B - a_{5}A - a_{1}AV\\ \frac{dB}{dt} &= I_2 + a_{3}V - a_{4}B - a_{6}B \end{align}\]
Take the time to identify each term and think about the biology or physics that might govern each term.
5.3 Paramaterization
Parameteriztion is what we call assigning numerical values to mathematical parameters. Here, we find initial estimates for the parameters in our model. We use the literature for this purpose (Bormann, Likens, and Melillo 1977).
If we have the data (we do) and relatively simple mathematical forms (we do), it is fairly straightforward to estimate parameters. For instance, we decided that net mineralization would be directly proportional to the size of the organic pool, \(B\), that is, \(F_4 = a_4B\). To calculate the annual incremental rate \(a_4\), we substitute data where we can, and solve what we need.
This example shows the loss of N from the bound pool due to net mineralization: \[\begin{align*} F_4 &= a_4 B\\ 69.6 &= a_4 B\\ a_4 &= \frac{-69.6}{4700}\\ a_4 &\approx -0.0148 \end{align*}\]
We use the same approach for second order equations as well, this time, the gain of N added to vegetation. \[\begin{align*} F_1 &= a_1 AV \\ 79.6 &= a_1 26\cdot 532 \\ a_1 &= \frac{79.6}{26\cdot 532}\\ a_1 &\approx 0.0058 \end{align*}\]
5.3.1 Instantaneous rates
Continuous differential equations describe instantaneous rates of change through time. To create instantaneous rate constants, we take advantage of a result from calculus. It turns out that, with some reasonable assumptions, the natural logarithm of the ratio of masses gives us an estimate of an average instantaneous rate.
Let \(B_0\) be the mass of N in the soil at time 0, and \(B_1\) would be the mass one year later if we summed \(B\) plus the flux coming out of \(B\): \[B_0=4700 \quad; \quad B_1 = B_0 + F_4 = 4700 - 69.6\] The average instantaneous rate, \(\alpha_4\) required to get us from \(B_0\) to \(B_1\) in one year is \[\alpha_4 = \log\left(\frac{B_1}{B_0}\right) = \log\left(\frac{4700-69.6}{4700}\right) \approx -0.0149\]
If you compare the annual incremental rate we first calculated to this instantaneous rate, you can see they are quite similar. They would be indistinguishable given the other uncertainties in actually estimating these fluxes and pools. However, that is not always the case.
| p.or.V | units | Estimate |
|---|---|---|
| \(A, B, V\) state variables | \(\frac{kg}{ha}\) = kg ha\(^{-1}\) | \(26, 4700, 532\) |
| \(a_1\), uptake rate by V from A | (kg ha\(^{-1}\))\(^{-1}\) y\(^{-1}\) | \(\log( (79.6 + 26 \cdot 532) / (26 \cdot 532) ) = 0.0057\) |
| \(a_2\), loss rate from V to A | y\(^{-1}\) | \(\log( (532-6.6 - 0.8 ) / 532 ) = -0.014\) |
| \(a_3\), loss rate from V to B | y\(^{-1}\) | \(\log( (532-54.2 - 2.7 - 0.1 - 6.2 ) / 532) = -0.0126\) |
| \(a_4\), mineralization | y\(^{-1}\) | \(\log( (4700-69.6) / 4700) = -0.0149\) |
| \(a_5\), export from A | y\(^{-1}\) | \(\log( (26-3.9) / 26) = -0.162\) |
| \(a_6\), export from B | y\(^{-1}\) | \(\log( (4700-0.1)/4700) = -0.000021\) |
| \(I_1\), bulk precip | kg ha\(^{-1}\) y\(^{-1}\) | \(6.5\) |
| \(I_2\), N fixation | kg ha\(^{-1}\) y\(^{-1}\) | \(14.2\) |
5.3.2 A sign of the times
When we estimate and use model parameters we need to be very conscious of the sign of the interaction. For instance, when we estimated the loss of N from the bound pool, the number we calculated was a negative number (\(a_4=-0.0149\)). When we use negative numbers, should we add them or subtract them?
Adding negative numbers is the same as subtracting positive numbers. So, if \(a_3 = -a_2\), then these two equations are the same: \[\frac{dX}{dt}=a_1 - a2 \quad ; \quad \frac{dX}{dt}=a_1+a_3\] Convince yourself that this is true.
We just have to be careful of signs.
Next we estimate the magnitude of each parameter in R. Recall that the absolute value of a number is symbolized with vertical lines \(|x|\). That value is its magnitude and is always positive. In what follows, we will use the absolute value for every parameter. This will allow us to use signs (+, -) in or equations that make intuitive sense to us. In R, the absolute value function is abs().
N Uptake by plants is a positive number.
Throughfall and inorganic exudates is a loss from vegetation, and therefore a negative number. Therefore, we will use its absolute value.
Litter, throughfall, organic exudates is a loss from vegetation, and therefore a negative number. Therefore, we will use its absolute value.
Net mineralization is a loss from the bound pool, and therefore a negative number. Therefore, we will use its absolute value.
Export from the available pool is a loss, and therefore a negative number. Therefore, we will use its absolute value.
Export from the bound pool is a loss, and therefore a negative number. Therefore, we will use its absolute value.
Here we create a single vector of all of the parameters, adding imports as well.
params <- c(
i1 = 6.5, # precip
i2 = 14.2, # fixation
a1 = a1, # uptake
a2 = a2, # throughfall and inorganic exudates
a3 = a3, # litter, throughfall, organic exudates
a4 = a4, # net mineralization
a5 = a5, # export from available
a6 = a6 #export from bound
) # close parentheses
params## i1 i2 a1 a2 a3 a4 a5 a6
## 6.500000e+00 1.420000e+01 5.738276e-03 1.400742e-02 1.264673e-01 1.491925e-02 1.625189e-01 2.127682e-055.4 Mathematical solution
The mathematical solution is the process of making the predictions using our model and our parameters. We solve the model. With simple models, we can sometimes find analytical solutions. For most ecosystem models, we have to solve the models numerically using numerical integration.
Here we write a function that includes our system of differential equations. This will allow R to integrate change through time.
bormann1 <- function(t, y, p) {
# time, vector of state variables and parameters must be in this order
# we can use as.list for both the state variables and parameters
# a1 = uptake
# a2 = loss from veg to avail
# a3 = loss from veg to bound
# a4 = net mineralization
# a5 = export from avail
# a6 = export from bound
with( as.list( c(y, p) ), {
dV.dt <- a1 * A * V - a2 * V - a3 * V
dA.dt <- i1 + a2 * V + a4 * B - a1 * A * V - a5 * A
dB.dt <- i2 + a3 * V - a4 * B - a6 * B
# Here we return a LIST whose first element is the vector of
# rates of change for the state variables. The first element must be these rates,
# in the same order as the state variables in y
# The second element, total, is the total N in the system
return(list( c(dV.dt, dA.dt, dB.dt),
total = V + A + B
) )})
}Now that we have the function, we tell R what to do with it. We will define the initial state of the system, and then tell R which time point we want it to return.
The initial state of the system is the set of starting values for the state variables. We could choose any values, but I select the values given in Bormann, Likens, and Melillo (1977).
Finally, let’s solve the system, and have R return the first 20 years.
time <- 0:20
out <- ode(y = initial.state, times=time, func=bormann1, parms = params)
head(out) # the first 6 lines## time V A B total
## [1,] 0 532.0000 26.00000 4700.000 5258.000
## [2,] 1 536.8480 26.03575 4711.481 5274.364
## [3,] 2 541.4532 25.90139 4723.389 5290.744
## [4,] 3 545.6897 25.77859 4735.675 5307.144
## [5,] 4 549.5990 25.67270 4748.291 5323.562
## [6,] 5 553.2241 25.58149 4761.191 5339.996Use pivot_longer() and ggplot() to make a graph. We use pivot_longer() gather multiple columns into one with a new name (values_to=kg.N), keeping track of the names of the original columns in a new column (names_to=State.var). We can use pivot_wider() if we ever want to spread those columns back out.
outL <- out %>% # select the data set
as.data.frame() %>% # make sure it is a data frame and not a matrix
## and the rearrange
pivot_longer( cols=-time, names_to="State.var", values_to="kg.N")
## plot the dynamics
ggplot(outL, aes(x=time, y=kg.N)) + # select variables to plot
geom_line() + # select the form of the graph
facet_wrap(~State.var, scale="free_y") # separate each state variable and plot each on its on scale.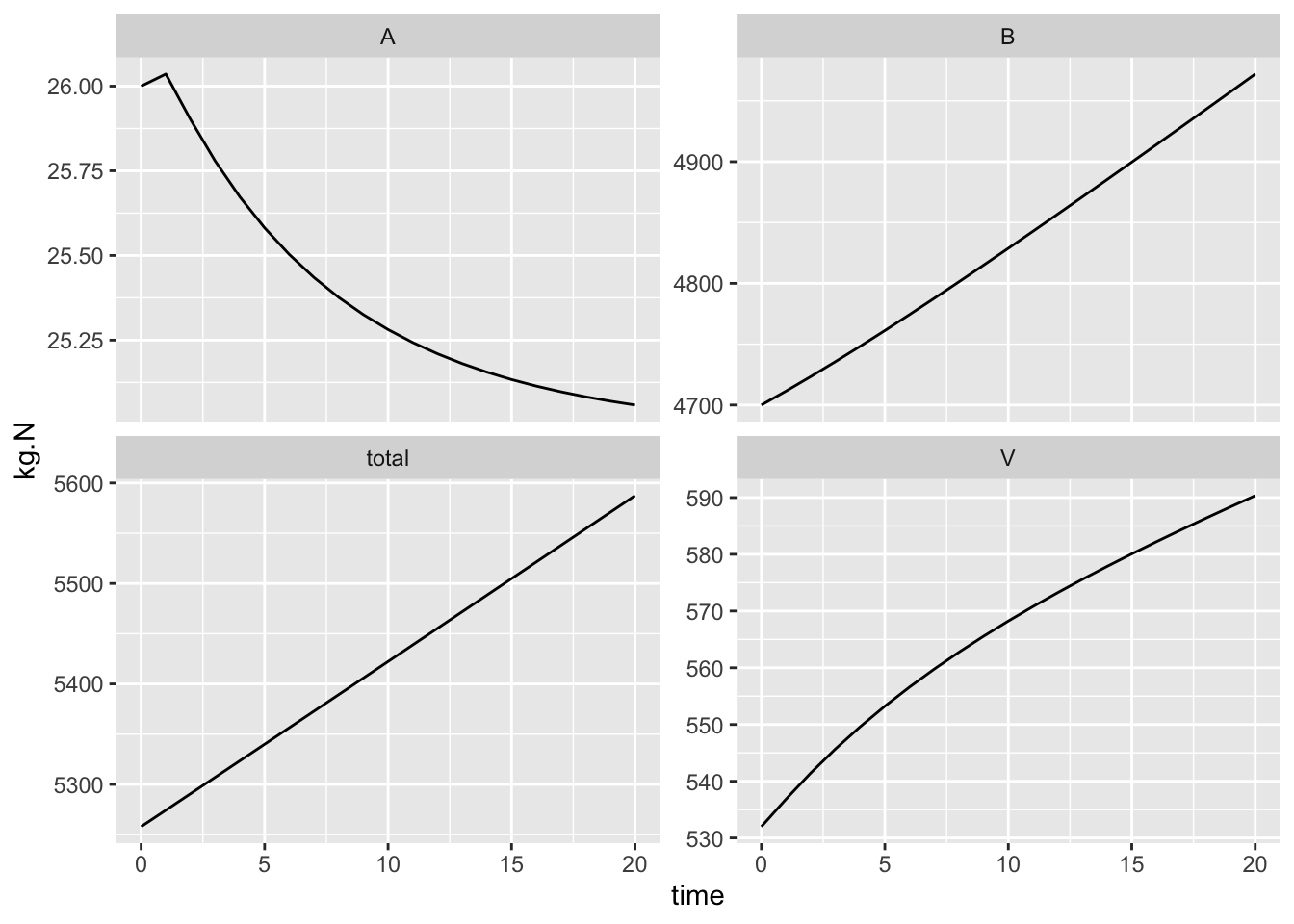
Figure 5.3: Dynamics of a simple N budget, based on Bormann et al. (1977).
In some ways, we have been moderately successful in our first pass at converting a purely budgetary model into a dynamic process model. We mimicked total load, and see similar changes through time of all the state variables.
Questions to ponder
We replicated approximately the N budget of Bormann et al. (1977), but clearly vegetation cannot keep accumulating N indefinitely.
What are our next steps?
5.5 Add self-limitation
One logical step is to assume that as vegetation eventually gets limited by some factor or resource that is not in our model. If, at first approximation, the vegetation reaches a carrying capacity independent of high resource availability, we can use an approximation suggested by Soetaert and Hermann (2009) for self-limitation, \[f(X)V\left(1-\frac{V}{K}\right)\] where \(f(X)\) is everything else that regulates mass-specific growth rate.
Exercise
Include self-limitation in your model of vegetation, estimate \(K\), and produce output.
Remember that following our template, we have a maximum rate times resource and self limitation, and inhibition. Currently, we have \[\frac{dV}{dt} = a_{1}AV - a_{2}V - a_3 V\] and rearranging, \[\frac{dV}{dt} = \left(a_{1}A - a_{2} - a_3\right) V\] If we add self-limitation, we get \[\frac{dV}{dt} = \left(a_{1}A - a_{2} - a_3\right) V \left(1-\frac{V}{K}\right)\] where \(K\) is the maximum amount of live vegetation that the ecosystem can sustain, in kg,N,ha\(^{-1}\). We don’t know exactly what that is yet, but we may be able to get estimates from the literature. For know we can pretend that it is just a bit more than was there in the mid-1970s, say, \(K=600\).
Now we rewrite the R function with self-limitation.
bormann2 <- function(t, y, p) {
# time, vector of state variables and parameters must be in this order
# we can use as.list for both the state variables and parameters
# a1 = uptake
# a2 = loss from veg to avail
# a3 = loss from veg to bound
# a4 = net mineralization
# a5 = export from avail
# a6 = export from bound
with( as.list( c(y, p) ), {
dV.dt <- (a1 * A - a2 - a3) * V * (1-V/K)
dA.dt <- i1 + a2 * V + a4 * B - a1 * A * V - a5 * A
dB.dt <- i2 + a3 * V - a4 * B - a6 * B
# Here we return a list whose first element is the vector of
# rates of change for the state variables. The first element must be these rates,
# in the same order as the state variables in y
# The second element is the total N in the system
return(list( c(dV.dt, dA.dt, dB.dt),
total = V + A + B
) )})
}We can add a new parameter to our vector of parameters, and then solve our new function bormann2 for the same time interval, and plot it.
params["K"] <- 600
## starting values in kg/ha
initial.state <- c( V = 532, A = 26, B = 4700)
time <- 0:200
out <- ode(y = initial.state, times=time, func=bormann2, parms = params)
outL2 <- out %>%
as.data.frame() %>%
pivot_longer(cols=-time, names_to="State.var", values_to="kg.N")
ggplot(outL2, aes(time, kg.N)) + geom_line() + facet_wrap(~State.var, scale="free_y")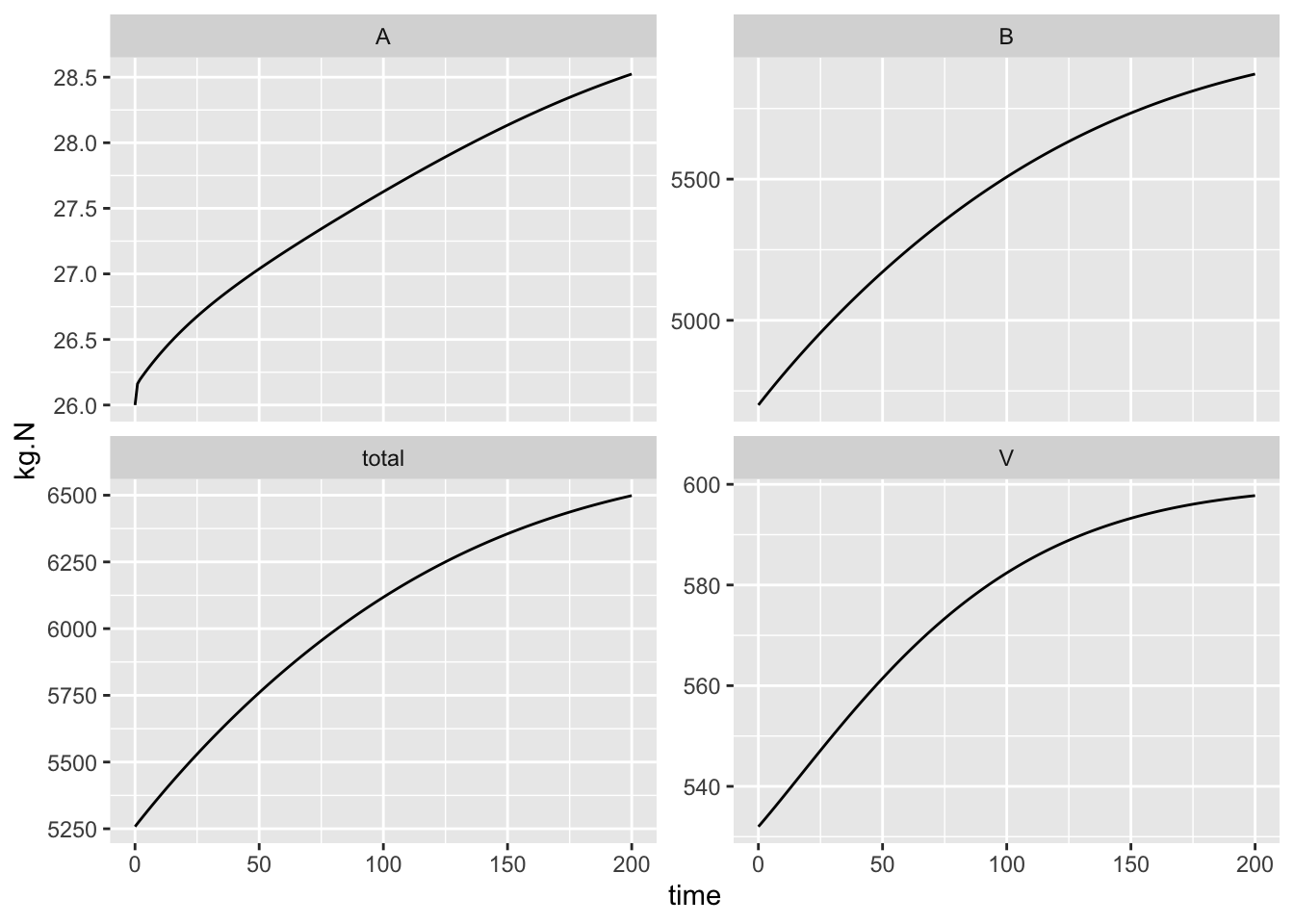
Figure 5.4: Dynamics of an N budget, assuming density-dependence in vegetation with a fixed carrying capacity (Bormann et al. 1977).
Unlike our first model of this system, we see state variables on curved trajectories and perhaps reaching asymptotes. This makes greater intuitive sense - over the short term, it is the same as the simple N budget shown in Bormann, Likens, and Melillo (1977) and it also shows a reasonable longterm trajectory for the vegetation, and the predicted consequences for the available and bound pools.
Save your own R script of ‘bormann2’
Make a new script that contains nothing but the bormann2 function. Copy the block of text where we define it, paste it into a new R script, and save it as bormann2.R. We will use this function in a latter section.